Most key tasks can be performed from the command line, and here we document all such functionality.
This is the multi-page printable view of this section. Click here to print.
Command Line Functionality
- 1: Input tags
- 2: Crystal Structure
- 3: General Utility for crystals
- 4: Symmetrizing displacements
- 5: Products of Irreducible Representations
- 6: Compute Irreducible Derivative
- 7: Phonon Linewidth and Thermal Conductivity
1 - Input tags
List of Input Tags
lattice_vectors
Testing 1 2 3
| type: | real, matrix |
| dimension: | 3x3 |
| scripts: | xx, yy |
type: matrix
dimension: 3x3
basis_atoms
| Name | Description |
|---|---|
| lattice_vectors | Lattice vectors in three dimensions, specified by a row-stacked 3x3 matrix. |
| basis_atoms | Basis atoms of crystal structure. |
| supa | A matrix of integers which left multiplies lattice_vectors to create a superlattice. |
| axial_strain | A vector of three floats which specifies the axial strain. |
| strain | A 3x3 real, symmetric matrix which specifies a general state of strain. |
| point_group | A string specifying the point group in Schoenfiles notation. |
| kpoint | A three dimensional vector specifying a kpoint. |
| qpoint | A three dimensional vector specifying a qpoint. |
| kpoint_mesh | A vector of three integers, specifying the kpoint mesh for electrons. |
| qpoint_mesh | A vector of three integers, specifying the qpoint mesh for phonons. |
| kpoint_path | A row stacked matrix of kpoints used to create a path through the BZ for plotting electronic bands. |
| qpoint_path | A row stacked matrix of qpoints used to create a path through the BZ for plotting phononic bands. |
| force_constants | A dictionary with keys being three dimensional vectors and values being NxN matrices, where N is the number of degrees of freedom in the unit cell. |
Tags with vector or matrix values
Many variables will be vectors or matrices, and all such variables will be processed by our text parser. Below are several examples which illustrate the variety of different ways that vectors may be input.
lattice_vectors:
[[0,0.5,0.5],
[0.5,0,0.5],
[0.5,0.5,0]]
lattice_vectors: |
0 1/2 1/2
1/2 0 1/2
1/2 1/2 0
lattice_vectors: 0 1/2 1/2; 1/2 0 1/2; 1/2 1/2 0
2 - Crystal Structure
For many different tasks performed in the PM suite, a crystal structure, or some component of a crystal structure, must be provided to the code. Most likely, this will be done using a yaml input file, and the two required key words are vec and atoms, which will contain the lattice vectors and the basis atoms, respectively. Considering the flourite structure, the most straightforward yaml file would be:
# xtal.yml
vec:
[[0.000000,2.764309,2.764309],
[2.764309,0.000000,2.764309],
[2.764309,2.764309,0.000000]]
atoms:
- Ca:
[[0,0,0]]
- F:
[[0.25,0.25,0.25],
[0.75,0.75,0.75]]
The code will infer that there is one basis atom labeled Ca and two basis atoms labeled F.
When entering matrices, we will always run the input through our general array parser (see parse_array if interested in the details). Therefore, there are many different options for entering a matrix as a string. For example, consider the following two examples:
scale: 2.764309
vec: |
0 1 1
1 0 1
1 1 0
atoms:
- Ca: |
0 0 0
- F: |
1/4 1/4 1/4
3/4 3/4 3/4
scale: 2.764309
vec: 0 1 1 ; 1 0 1 ; 1 1 0
atoms:
- Ca: 0 0 0
- F: 1/4 1/4 1/4 ; 3/4 3/4 3/4
where scale is a constant that multiplies all lattice vectors (a list of three constants could have been provided), and the vertical lines tells yaml to expect a text block. Our parser has a hierarchy of delimiters, ranging from space, comma, semicolon, newline. In the above example, we have two types of delimiters (i.e. spaces and newlines), which tells the code to form a matrix.
Warning
Potential Errors in yaml input
In the case of syntax error in YAML file, a RuntimeError will be thrown indicating the an error has
occurred during the YAML loading process. For example, with the following text as YAML input:
scale: 2.764309
vec: |
0 1 1 ; 1 0 1 ; 1 1 0
atoms:
- Ca: |
0 0 0
- F: |
1/4 1/4 1/4 ; 3/4 3/4 3/4
The following error message will appear:
RuntimeError: Following error occured processing input YAML string:
ScannerError: while scanning a simple key
in "<unicode string>", line 6, column 5
could not find expected ':'
in "<unicode string>", line 7, column 3
Prototype Crystal Structures
There are a number of very common crystal structures that are adopted in numerous compounds, such as rock salt, flourite, etc. There is a simple command line script to output these crystal structures.
$ pm-prototype-xtal --perovskite
# Crystal
vec:
[[ 3.91300000, 0.00000000, 0.00000000],
[ 0.00000000, 3.91300000, 0.00000000],
[ 0.00000000, 0.00000000, 3.91300000]]
atoms:
- Sr:
[[ 0.50000000, 0.50000000, 0.50000000]]
- Ti:
[[ 0.00000000, 0.00000000, 0.00000000]]
- O:
[[ 0.50000000, 0.00000000, 0.00000000],
[ 0.00000000, 0.50000000, 0.00000000],
[ 0.00000000, 0.00000000, 0.50000000]]
3 - General Utility for crystals
Here we provide some of the basic functionality for periodica. A crystal structure
file must be provided on the command line, either as a filename or as standard input.
The crystal structure is simply output if no other
commands are provided. Let us use pm-prototype to look at some examles.
# start with perovskite
pm-prototype-xtal --perovskite > xtal.yaml
pm-periodica xtal.yaml
# or we can simply do this
pm-prototype-xtal --perovskite | pm-periodica
In both cases, the output will be:
# Crystal
vec:
[[ 3.91300000, 0.00000000, 0.00000000],
[ 0.00000000, 3.91300000, 0.00000000],
[ 0.00000000, 0.00000000, 3.91300000]]
atoms:
- Sr:
[[ 0.50000000, 0.50000000, 0.50000000]]
- Ti:
[[ 0.00000000, 0.00000000, 0.00000000]]
- O:
[[ 0.50000000, 0.00000000, 0.00000000],
[ 0.00000000, 0.50000000, 0.00000000],
[ 0.00000000, 0.00000000, 0.50000000]]
Basic manipulations of the unit cell can be peformed, like shifting or permuting the atoms.
pm-periodica xtal.yaml --shift-origin 0.5,0.5,0.5 --shift-into-cell --permute-atoms 0,1,3,4,2
# Crystal
vec:
[[ 3.91300000, 0.00000000, 0.00000000],
[ 0.00000000, 3.91300000, 0.00000000],
[ 0.00000000, 0.00000000, 3.91300000]]
atoms:
- Sr:
[[ 0.00000000, 0.00000000, 0.00000000]]
- Ti:
[[ 0.50000000, 0.50000000, 0.50000000]]
- O:
[[ 0.50000000, 0.00000000, 0.50000000],
[ 0.50000000, 0.50000000, 0.00000000],
[ 0.00000000, 0.50000000, 0.50000000]]
Basic information about the lattice can be printed.
4 - Symmetrizing displacements
Here we illustrate how to symmtrize displacements at a given q-point according to irreducible representations of the little group using the script pm-disp-qrep. Take the example of \(\bm{q}=(\frac{1}{2},\frac{1}{2},\frac{1}{2})\) in cubic SrTiO\(_3\). We will use pm-prototype-xtal to generate the crystal structure file.
$ pm-prototype-xtal --perovskite > xtal.yml
Printing out the irreducible representations, we have
$ pm-disp-qrep xtal.yml --point-group Oh --qpoint 1/2,1/2,1/2 --print-irreps
OrbitKey(name='Sr', index=0) [0]
T2g
OrbitKey(name='Ti', index=0) [0]
T1u
OrbitKey(name='O', index=0) [0, 1, 2]
A1g+Eg+T1g+T2g
We can also print out the irreducible representation vectors.
$ pm-disp-qrep xtal.yml --point-group Oh --qpoint 1/2,1/2,1/2 --print-vectors
T2g[Sr]
0.0000 0.0000 1.0000
1.0000 0.0000 0.0000
0.0000 1.0000 0.0000
T1u[Ti]
1.0000 0.0000 0.0000
0.0000 1.0000 0.0000
0.0000 0.0000 1.0000
A1g[O]
0.5774 0.0000 0.0000 0.0000 0.5774 0.0000 0.0000 0.0000 0.5774
Eg[O]
0.7071 0.0000 0.0000 0.0000 -0.7071 0.0000 0.0000 0.0000 0.0000
-0.4082 0.0000 0.0000 0.0000 -0.4082 0.0000 0.0000 0.0000 0.8165
T1g[O]
0.0000 0.0000 0.0000 0.0000 0.0000 0.7071 0.0000 -0.7071 0.0000
0.0000 0.0000 -0.7071 0.0000 0.0000 0.0000 0.7071 0.0000 0.0000
0.0000 0.7071 0.0000 -0.7071 0.0000 0.0000 0.0000 0.0000 0.0000
T2g[O]
0.0000 0.7071 0.0000 0.7071 0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.7071 0.0000 0.7071 0.0000
0.0000 0.0000 0.7071 0.0000 0.0000 0.0000 0.7071 0.0000 0.0000
This script will block diagonalize a dynamical matrix which has been provided. Consider the dyanmical matrix at the gamma point for STO:
$ cat dmat.yaml
dynamical_matrix_real:
3.6228 0 0 -2.990 0 0 0.2751 0 0 0.2751 0 0 -1.1822 0 0
0 3.6228 0 0 -2.990 0 0 -1.1822 0 0 0.2751 0 0 0.2751 0
0 0 3.6228 0 0 -2.990 0 0 0.2751 0 0 -1.1822 0 0 0.2751
-2.990 0 0 2.060 0 0 0.2442 0 0 0.2442 0 0 0.4416 0 0
0 -2.990 0 0 2.060 0 0 0.4416 0 0 0.2442 0 0 0.2442 0
0 0 -2.990 0 0 2.060 0 0 0.2442 0 0 0.4416 0 0 0.2442
0.2751 0 0 0.2442 0 0 4.0322 0 0 0.90 0 0 -5.460 0 0
0 -1.1822 0 0 0.4416 0 0 11.6616 0 0 -5.460 0 0 -5.460 0
0 0 0.2751 0 0 0.2442 0 0 4.0322 0 0 -5.460 0 0 0.90
0.2751 0 0 0.2442 0 0 0.90 0 0 4.0322 0 0 -5.460 0 0
0 0.2751 0 0 0.2442 0 0 -5.460 0 0 4.0322 0 0 0.90 0
0 0 -1.1822 0 0 0.4416 0 0 -5.460 0 0 11.6616 0 0 -5.4605
-1.1822 0 0 0.4416 0 0 -5.460 0 0 -5.460 0 0 11.6616 0 0
0 0.2751 0 0 0.2442 0 0 -5.460 0 0 0.90 0 0 4.0322 0
0 0 0.2751 0 0 0.2442 0 0 0.90 0 0 -5.460 0 0 4.0322
We can then block diagonalize as follows:
pm-prototype-xtal --perovskite2 | pm-disp-qrep --point-group Oh --qpoint 0,0,0 --dynamical-matrix ~/dmat.yaml
T1u-block : [('T1u', 0), ('T1u', 1), ('T1u', 2), ('T1u', 3)]
Dynamical matrix sub-block - first row
[[ 0. 0. 0. 0. ]
[ 0. 2.57 3.2 -0.18]
[ 0. 3.2 3.01 -1.33]
[ 0. -0.18 -1.33 16.7 ]]
Mass matrix sub-block - first row
[[ 36.7 5.59 -27.74 0. ]
[ 5.59 45.08 13.87 0. ]
[-27.74 13.87 69.71 0. ]
[ 0. 0. 0. 16. ]]
Mass renormalized Eigvecs
[[-0.324 0.931 -0.169 -0.017]
[ 0.692 0.111 -0.713 0. ]
[-0.644 -0.348 -0.68 -0.046]
[-0.035 0. -0.034 0.999]]
Unique Frequencies (meV)
[-8.19 -0.58 19.56 66.13]
T2u-block : [('T2u', 0)]
Dynamical matrix sub-block - first row
[[3.13]]
Mass matrix sub-block - first row
[[16.]]
Mass renormalized Eigvecs
[[1.]]
Unique Frequencies (meV)
[28.61]
It may be desirable to perform a unitary transformation within some irreducible representation subspace. Consider a yam file called unitary.yaml with the following content:
# unitary transformation to nearly diagonize the T1u subspace
- block: ['Optical',0]
irr_rep: 'T1u'
instances: [0,1]
U:
[[ -0.73059222, 0.68281403 ],
[ 0.68281403, 0.73059222 ]]
The conventional output is:
$ pm-prototype-xtal --perovskite2 | pm-disp-qrep --point-group Oh --qpoint 0,0,0 --print-vectors
('Acoustic', 0) [0, 1, 2, 3, 4]
T1u
('T1u', 0)
[[0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. ]
[0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. ]
[0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447 0. 0. 0.447]]
('Optical', 0) [0, 1, 2, 3, 4]
2T1u
('T1u', 0)
[[-0.224 0. 0. 0.894 0. 0. -0.224 0. 0. -0.224 0. 0. -0.224 0. 0. ]
[ 0. -0.224 0. 0. 0.894 0. 0. -0.224 0. 0. -0.224 0. 0. -0.224 0. ]
[ 0. 0. -0.224 0. 0. 0.894 0. 0. -0.224 0. 0. -0.224 0. 0. -0.224]]
('T1u', 1)
[[-0.866 0. 0. 0. 0. 0. 0.289 0. 0. 0.289 0. 0. 0.289 0. 0. ]
[ 0. -0.866 0. 0. 0. 0. 0. 0.289 0. 0. 0.289 0. 0. 0.289 0. ]
[ 0. 0. -0.866 0. 0. 0. 0. 0. 0.289 0. 0. 0.289 0. 0. 0.289]]
('O', 0) [2 3 4]
T1u+T2u
('T1u', 0)
[[ 0.408 0. 0. 0.408 0. 0. -0.816 0. 0. ]
[ 0. -0.816 0. 0. 0.408 0. 0. 0.408 0. ]
[ 0. 0. 0.408 0. 0. -0.816 0. 0. 0.408]]
('T2u', 0)
[[ 0. 0. 0.707 0. 0. 0. 0. 0. -0.707]
[-0.707 0. 0. 0.707 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. -0.707 0. 0. 0.707 0. ]]
Now we can print the relevant output after the unitary transformation:
$ pm-prototype-xtal --perovskite2 | pm-disp-qrep --point-group Oh --qpoint 0,0,0 --unitary-transformation ~/unitary.yaml --print-vectors
('Optical', 0) [0, 1, 2, 3, 4]
2T1u
('T1u', 0)
[[-0.428 0. 0. -0.653 0. 0. 0.36 0. 0. 0.36 0. 0. 0.36 0. 0. ]
[ 0. -0.428 0. 0. -0.653 0. 0. 0.36 0. 0. 0.36 0. 0. 0.36 0. ]
[ 0. 0. -0.428 0. 0. -0.653 0. 0. 0.36 0. 0. 0.36 0. 0. 0.36 ]]
('T1u', 1)
[[-0.785 0. 0. 0.611 0. 0. 0.058 0. 0. 0.058 0. 0. 0.058 0. 0. ]
[ 0. -0.785 0. 0. 0.611 0. 0. 0.058 0. 0. 0.058 0. 0. 0.058 0. ]
[ 0. 0. -0.785 0. 0. 0.611 0. 0. 0.058 0. 0. 0.058 0. 0. 0.058]]
Given some distorted crystal structure, one can project the displacement onto symmetrized displacements. Consider the primitive unit cell of STO where the ferroelectric mode is allowed to condense by treating the nuclear motion as classical:
$ cat xtal_ferro.yaml
# Crystal
vec:
[[ 3.89736730, 0.00092044, 0.00092044],
[ 0.00092044, 3.89736730, 0.00092044],
[ 0.00092044, 0.00092044, 3.89736730]]
atoms:
- Sr:
[[ 0.02422827, 0.02422827, 0.02422827]]
- Ti:
[[ 0.52563170, 0.52563170, 0.52563170]]
- O:
[[ 0.51647453, 0.01719097, 0.51647453],
[ 0.51647453, 0.51647453, 0.01719097],
[ 0.01719097, 0.51647453, 0.51647453]]
Projecting onto irreducible representations gives:
pm-prototype-xtal --perovskite2 | pm-disp-qrep --point-group Oh --qpoint 0,0,0 --unitary-transformation unitary.yaml --project-xtal xtal_ferro.yaml
Projection onto irreducible representations
Block : Acoustic
----------------
T1u 0.1744 0.1744 0.1744
Block : Optical
---------------
T1u -0.0353 -0.0353 -0.0353
1.T1u -0.0018 -0.0018 -0.0018
Block : O
---------
T1u -0.0023 -0.0023 -0.0023
T2u 0 0 0
5 - Products of Irreducible Representations
A common group theoretical task is the direct product or symmetric direct product of irreducible representations. The composition of a product is obtained as
$ pm-irr_rep_product --point-group Oh --irr-reps T2g,T2g
# T2gxT2g = A1g+Eg+T1g+T2g
The composition of a symmetric product is obtained as
$ pm-irr_rep_product --point-group Oh --irr-reps T2g,T2g --symmetric
# [T2gxT2g] = A1g+Eg+T2g
An arbitrary number of irreps can be handled
$ pm-irr_rep_product --point-group Oh --irr-reps T2g,T2g,Eg,Eg,A2g
# T2gxT2gxEgxEgxA2g = 2A1g+2A2g+4Eg+4T1g+4T2g
Another important task is constructing the irreducible representation vectors of the product representation in terms of the rows of the original irreducible representations.
$ pm-irr_rep_product --point-group Oh --irr-reps Eg,Eg --print-irr-vectors
# EgxEg = A1g+A2g+Eg
#
# irr Eg.0xEg.0 Eg.0xEg.1 Eg.1xEg.0 Eg.1xEg.1
# A1g 0.7071 0.0 0.0 0.7071
# A2g 0.0 0.7071 -0.7071 0.0
# Eg.0 0.0 0.7071 0.7071 0.0
# Eg.1 0.7071 0.0 0.0 -0.7071
The same can be done for the symmetric product
$ pm-irr_rep_product --point-group Oh --irr-reps Eg,Eg --print-irr-vectors --symmetric
# [EgxEg] = A1g+Eg
#
# irr Eg.0xEg.0 Eg.0xEg.1 Eg.1xEg.1
# A1g 0.7071 0.0 0.7071
# Eg.0 0.0 1.0 0.0
# Eg.1 0.7071 0.0 -0.7071
It might also be useful to print out the transpose of the results, which can be done with the print-transpose flag:
$ pm-irr_rep_product --point-group Oh --irr-reps Eg,Eg --print-irr-vectors --symmetric --print-transpose
# [EgxEg] = A1g+Eg
#
# A1g Eg.0 Eg.1
# Eg.0xEg.0 0.7071 0.0000 0.7071
# Eg.0xEg.1 0.0000 1.0000 0.0000
# Eg.1xEg.1 0.7071 0.0000 -0.7071
In many cases, one is only concerned with the identity representation, and the flag only-print-identity will only print identity representations and will prune out any basis vectors that are not contained in the product:
$ pm-irr_rep_product --point-group Oh --irr-reps Eg,Eg --print-irr-vectors --symmetric --only-print-identity
# [EgxEg] = A1g+Eg
#
# Eg.0xEg.0 Eg.1xEg.1
# A1g 0.7071 0.7071
6 - Compute Irreducible Derivative
Within this package we can compute irreducible derivatives of phonons and phonon interactions at a given order with either LID or BID approach. The theory behind these approaches are described in the following paper:
Specifically, we can execute the LID, SS-BID and HS-BID approaches from the command line using the following commands:
pm-lid-mesh: compute irreducible derivatives of a given FTG and order using LID method;pm-bid: compute irreducible derivatives of a given FTG and order using SS-BID method;pm-hsbid: compute irreducible derivatives of a given FTG and order using HD-BID method.
These commands take in generally the same command line options, therefore one can switch between approaches by changing the command while keeping
the options the same.
For example, below is guide on using the LID approach to compute irreducible derivatives of NaCl at second order but one can replace pm-lid-mesh
with pm-bid or pm-hsbid to execute SS-BID or HS-BID approach.
LID Approach on NaCl at Second Order
There are many ways to use this package to execute calculations of the irreducible derivatives with LID approach. Here we demonstrate a recommended workflow to execute our LID approach at second order on NaCl from forces computed by first principle method.
Symmetry Analysis and Find the Measurements to Compute
First we create a file xtal.yml describing the structure of NaCl:
# xtal.yml
vec:
[[ 0.00000000, 2.83000729, 2.83000729],
[ 2.83000729, 0.00000000, 2.83000729],
[ 2.83000729, 2.83000729, 0.00000000]]
atoms:
- Na:
[[ 0.00000000, 0.00000000, 0.00000000]]
- Cl:
[[ 0.50000000, 0.50000000, 0.50000000]]
Then, with this structure and the point group \(O_h\), we can write the minimal configuration file, named config.yml, to execute the LID approach with a supercell \(\hat{S}_{BZ}=2\hat1\):
# config.yml
structure: 'xtal.yml'
supa: |
2 0 0
0 2 0
0 0 2
pg: 'Oh'
order: 2
full_symmetry: True
delta: [ 0.02, 0.03, 0.04]
There are numerous parameters which have default settings that can be changed, and these can be added to the config.yml file listed above:
fdtype: 'c'
root_directory: '.'
database: 'database.db'
db_type: 'sqlite'
db_table: 'lid_phonon'
With the configuration file we can initiate the pre-processing step which will execute the symmetry analysis and create the jobs that need to be computed with first principles:
pm-lid-mesh --config config.yml --create
The above step will create two files:
lid_mesh.hdf5: A HDF5 file containing the computed symmetry analysis results, which will be used in the post-processing step to compute the irreducible derivatives after first principle calculations are finished.database.db: A SQLite database file containing the jobs need to be computed with first principle calculations (db_typeis specified to be ‘sqlite’ in theconfig.ymlfile, other database can be used if a working interface is provided).
Note
The above steps can also be executed purely in command line with the following command:
pm-lid-mesh --save-config --create --structure xtal.yml \
--supa '2,0,0;0,2,0;0,0,2' --pg Oh --order 2 --full-symmetry \
--delta 0.02,0.03,0.04 --fdtype c --database database.db \
--db-type sqlite --db-table lid_phonon
Prepare and Execute First Principle Calculations
The next step is to create the first principle jobs to be computed, the package generically supports all types of first principle compute engines provided a working interface, and here we demonstrate using VASP. We begin by create the VASP jobs to be executed:
pm-jobs --config config.yml --create --engine vasp --save-config jobs_config.yml \
--job-config-path path-to-vasp-input-templates --root-directory jobs-ro-run
Inside the path-to-vasp-input-templates directory, one usually needs to provide “INCAR”, “KPOINTS” and “POTCAR” files and they will be used as templates when creating the
vasp jobs, each vasp job will be created in a separate directory for convenience. Once these directories are created, VASP can be executed within each directory.
Afterwards, the calculation results can be collected and stored in the database:
pm-jobs --config jobs_config.yml --retrieve
Note
We initiated thepm-jobs command with the input configuration file for the LID analysis config.yml,
and subsequently saved a new configuration file jobs_config.yml for the pm-jobs code for the purpose of convenience.
These configuration files contains all the input arguments that are required to reproduce the exact same setup.Compute Irreducible Derivatives from the Results of First Principle Calculations
Finally, we can execute the post-processing step of the LID approach to compute the irreducible derivatives and, for example, compute the force constants tensors for Fourier interpolation:
pm-lid-mesh --load-lid-mesh lid_mesh.hdf5 --config config.yml \
--post --save-fi --save-ids --save-dts
If the material of interest is an insulator and the dipole-dipole interaction needs to be considered, the dataset for computing the dipole-dipole interaction needs to be provided as an input as well:
pm-lid-mesh --load-lid-mesh lid_mesh.hdf5 --config config.yml --epsilon path-to-epsilon.yml \
--post --save-fi --save-ids --save-dts
The dataset for computing the dipole-dipole interaction can be computed from first principle methods.
Continuing with the VASP example, we can obtain the dataset by executing a static calculation adding LEPSILON=.TRUE. to the “ICNAR” file.
Once the calculation is finished, use the following command inside the calculation directory to parse the output from VASP and create the epsilon.yml file:
pm-epsilon --vasp -o epsilon.yml .
then replace path-to-epsilon.yml with the path to the generated epsilon.yml file.
The following files are created in this step:
irreducible_derivatives.hdf5: A HDF5 files containing the names of the irreducible derivatives and their values.fourier_interpolation.hdf5: A HDF5 files containing all the necessary information (structure, force constants tensors, FTG and dipole-dipole contributions if at second order) to compute Fourier interpolation.dynamic_tensors.hdf5: A HDF5 files containing all the dynamic tensors in the naive basis within irreducible Q.
Note
Both BID and HS-BID approaches can be executed following the exact same workflow while replacing the commandpm-lid-mesh
with pm-bid and pm-hsbid respectively, and a change of the table name for the database is also recommended (e.g. change to ‘bid_phonon’).Computing and analyzing error tails
The results of any finite displacement approach are only reliable if the discretization error has been properly controlled. Forward and backward finite difference guarantee a linear error tail, while central finite difference guarantees a quadratic error tail. Resolving the error tail is a sure sign that the discretization error has been properly extrapolated to zero. For phonons, we will be taking either the first derivatives of the forces or the second derivatives of the energy, which are typically not sensitive. Therefore, it is common practice to use a single finite displacement (i.e. a single delta), and then there is nothing to analyze. However, there are plenty of situations where one does find sensitive results, such as metallic systems with Fermi surface nesting or even band insulators when using the SCAN functional. If one computes three or more deltas, then the error tail can be scrutinized to judge the quality of the result.
To examine the error tails, the corresponding data must be output during the post-processing of results. The above lid-mesh commands needs the –err-output flag as follows:
pm-lid-mesh --load-lid-mesh lid_mesh.hdf5 --config config.yml \
--post --save-fi --save-ids --save-dts --err-output error_tails.hdf5
The next step is extract the results from the hdf5 file and output them to individual yaml files:
pm-convert-errortail error_tails.hdf5
The yaml files can then be plotted to PDF files. For example:
pm-plot-errortail 1_0_errortail.yml --iscomplex --output 1_0_errortail.pdf
At present, one can execute a loop in bash over all the files:
for i in *_errortail.yml; do
echo $i
pm-plot-errortail $i --iscomplex --output $(basename $i .yml).pdf
done
Computing phonon dispersion and DOS
With the fourier_interpolation.hdf5 file obtained at second order, we can compute phonon dispersion and density of states (DOS).
Let’s continue the NaCl example and first prepare the configuration file phonon_config.yml for computing the phonon dispersion and DOS:
# phonon_config.yml
band:
- ['0 0 0', '1/2 1/2 0']
- ['-1/2 1/2 0', '0 0 0']
- ['0 0 0', '1/2 1/2 1/2']
band_label:
- $\Gamma$
- X
- $\Gamma$
- L
mesh: 20 20 20
Then we can execute the following command to compute the band structure and DOS:
pm-phonon-band-dos --load-fi fourier_interpolation.hdf5 --config phonon_config.yml \
--save-band --save-grid --save-dos --save-plot
The following files are created in this step:
band_plot_config.yml: A YAML file with the configuration the plot the band structure and DOS;bands.dat: A text file with the phonon band structure data computed with Fourier interpolation;grid_phonons.dat: A text file with the data of the phonons that are measured at the FTG that fall on the path in the plot;dos.dat: A text file with the data of phonon DOS.
We can plot the phonon band structure and DOS with the following command:
pm-plot-band -s band_plot_config.yml
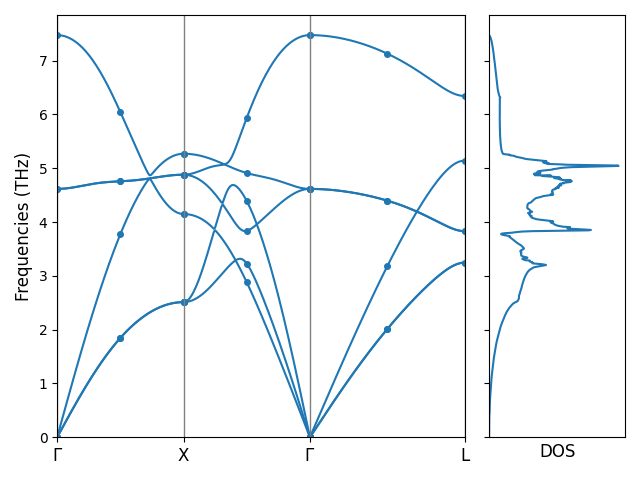
Phonon bands and DOS of NaCl
7 - Phonon Linewidth and Thermal Conductivity
Second and third order irreducible derivatives must be computed first, as described here, and the second and third order force constants may then be used to predict the phonon linewidth using perturbation theory. The phonons and the linewidths can then be used to computed thermal conductivity with the relaxation time approximation.
Phonon Linewidth
Here we continue the NaCl example from before.
First, we need to prepare a configuration file config.yml for the pm-conductivity command:
# config.yml
structure: xtal.yml
load_fi2: fi_order2.hdf5
load_fi3: fi_order3.hdf5
mesh: [11, 11, 11]
band:
- ['0 0 0', '1/2 1/2 0']
- ['-1/2 1/2 0', '0 0 0']
- ['0 0 0', '1/2 1/2 1/2']
band_label:
- $\Gamma$
- X
- $\Gamma$
- L
where:
xtal.ymlcontains structure of NaCl;fi_order2.hdf5is the HDF5 data file for the FourierInterpolation class at second order, which contains the 2nd order force constants;fi_order3.hdf5is the HDF5 data file for the FourierInterpolation class at third order, which contains the 3rd order force constants.
In this example, we use the FourierInterpolation object of a \(\hat{S}_{BZ}=4\hat{\mathbf{1}}\) FTG (i.e. a \(4 \times 4 \times 4\) supercell) at second order and the FourierInterpolation object of a \(\hat{S} _{BZ}=2\hat{\mathbf{1}}\) FTG (i.e. a \(2 \times 2 \times 2\) supercell) at third order. We interpolate the phonons and phonon interactions to the mesh of \(11\hat{\mathbf{1}}\), and compute the linewidth along the K-path \(\Gamma \to X \to \Gamma \to L\).
Execute the following command the compute the phonon linewidth:
pm-conductivity --config config.yml --save-gamma
Thermal Conductivity
Using the same NaCl example, we can prepare a configuration file config.yml similar to the one above:
# config.yml
structure: xtal.yml
load_fi2: fi_order2.hdf5
load_fi3: fi_order3.hdf5
mesh: [11, 11, 11]
Execute the following command the compute the thermal conductivity using relaxation time approximation (RTA):
pm-conductivity --config config.yml --save-kappa --mode RTA